Tématerületi Kiválósági Program
Mesterséges intelligencia, nagy hálózatok, adatbiztonság: matematikai megalapozás és alkalmazások
Rövid leírás
Kutatásaink alapját az iparban és szolgáltatásokban, ill. nem utolsó sorban az egészségügyben megjelenő technológiai igények jelentik. Itt a gépi látás, természetes nyelvfeldolgozás, hálózatelemzés, optimalizálás, szekvenciák (idősorok, naplóállományok) feldolgozása adják a fő irányokat. Ezen feladatok jelentős részében a state-of-the-art megoldásokat a gépi, azon belül a mély tanulás adja, így a gépi tanulás a javasolt tématerületi kutatásban meghatározó szerepet kap. A gépi tanulás egyik fontos és kurrens kutatási iránya a terület matematikai kapcsolódásainak kiaknázása. Ez egyrészt a gépi tanulás matematikai alapjainak megteremtését, a technológiák és képességeik jobb megértését, majd annak nyomán a technológia célirányos fejlesztését jelenti. Másrészt, megfordítva az alkalmazott matematikai területet és a gépi/mély tanulást összekapcsoló kutatás-fejlesztések irányát, a MI-t ma meghatározó technológiák megújíthatják az alkalmazott matematika több területét, mint a kombinatorikus optimalizálást, a differenciálegyenleteket, a sztochasztikus folyamatokat és a hálózatkutatást, ahol jellemzően komplex számítási feladatok hatékonyabban (gyorsabban, ill. pontosabban) lesznek megoldhatók a gépi/mély tanulás technológiái segítségével.
Kutatócsoportok

Adatbiztonság

Anyagtudomány
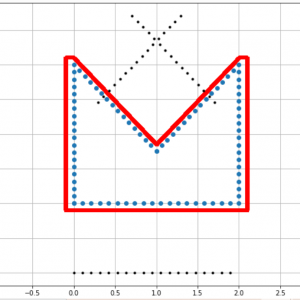
Differenciálegyenletek

Gépi tanulás matematikai alapjai

Hálózatok
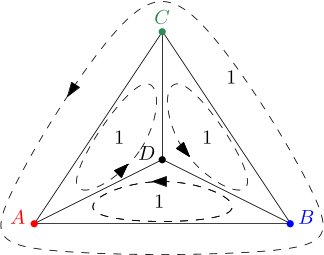
Kombinatorikus geometria
Mély tanulás gyakorlati alkalmazásai
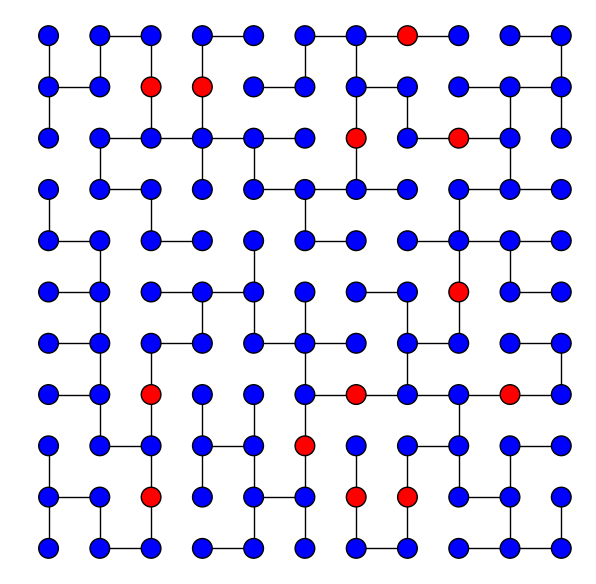
Optimalizálás
PIT Bioinformatikai csoport
Pénzügyi matematika
Kutatócsoportok témaleírásai

Adatbiztonság
A kutatási időszakban új, hierarchikus titokmegosztó sémákat tervezünk konstruálni, a konjunktív modellen belül. A tervezett konstrukció véges testek felett, geometriai jellegű technikákon alapszik, és új paraméter-értékekre ad megoldást.
Vezető:
Sziklai Péter
Tagok:
Villányi Viktória

Anyagtudomány
Témák: Lokális keménység meghatározása mikroszerkezeti jellemzők alapján konvolúciós neurális hálók segítségével, diszlokáció lavinák akusztikus emissziójának gépi tanulással történő előrejelzése, lokális folyásfeszültség meghatározása CNN alapú módszerekkel.
Vezető:
Ispánovity Péter Dusán
Tagok:
Berta Dénes, Péterffy Gábor, Ugi Gábor
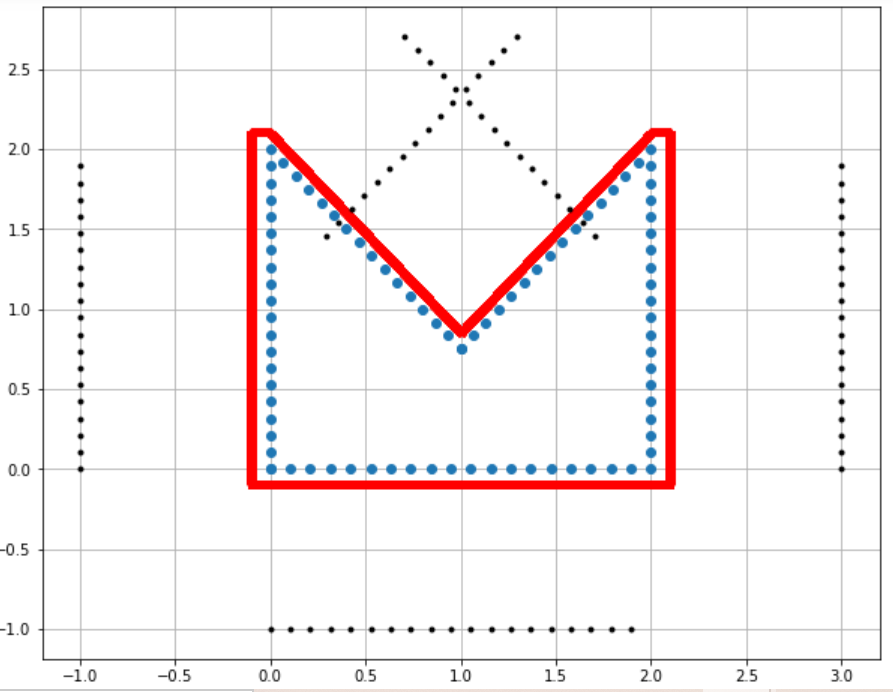
Differenciálegyenletek
A csoport célja a differenciálegyenletek és neurális hálók közötti kapcsolat mélyebb felfedezése. A csoport egyik iránya neurális hálók megértése differenciálegyenletek segítségével. A másik irány pedig neurális hálók alkalmazása parciális differenciálegyenletekkel kapcsolatos problémák numerikus megoldására.
Vezető:
Izsák Ferenc
Tagok:
Csomós Petra, Fekete Imre, Karátson János, Maros Gábor, Mogyorósi Bálint, Molnár András, Neogrády-Kiss Márton, Simon Péter, Tóth Árpád

Gépi tanulás matematikai alapjai
A kutatás célja többek között optimalizálási feladatok egzakt megoldásának felgyorsítása MI módszerek segítségével.
Vezető:
Lukács András
Tagok:
Bakos Bence, Hidy Gábor, Vas Bernadett, Zombori Zsolt, Csiszárik Adrián, Karl János

Hálózatok
Célunk a fertőzési ráta becslése egy kétrétegű véletlengráf-modellben, a klasszikus (maximum likelihood) és neurális hálózaton alapuló becslések összehasonlítása. Ezen belül azt vizsgáljuk, hogy a klaszterezettségi együttható hogyan befolyásolja az alkalmazott módszerek eredményességét.
Vezető:
Backhausz Ágnes
Tagok:
Bognár Edit, Csiszár Villő, Tarkányi Damján, Zempléni András

Kombinatorikus geometria
A kombinatorikus geometria struktúrái a gyakran fennálló strukturális hasonlóságok alapján ígéretes alanyai a tanulási algoritmusoknak. Ezen a módon megtámadhatónak gondoljuk a megoldatlan Hadwiger–Nelson problémát, a sík kromatikus számának meghatározását. Egy gépi tanuláson alapuló módszer jó eséllyel fel tudná mérni, hogy milyen típusú gráfokat érdemes használni, például a tört kromatikus szám értékére optimalizálva.
Vezető:
Pálvölgyi Dömötör
Tagok:
Ágoston Péter, Keszegh Balázs, Naszódi Márton, Jung Attila, Zólomi Kristóf

Mély tanulás gyakorlati alkalmazásai
Képfeldolgozás (orvosi alkalmazások), nyelvfeldolgozás mély tanulási modelljeinek bevezetése más, új alkalmazásokban, sztochasztikus folyamatok paraméterbecslése
Vezető:
Lukács András
Tagok:
Csiszárik Adrián, Csanády Bálint, Fischer Kornél, Ivkovic Iván, Kovács Dávid, Tóth-Lakits Dalma

Optimalizálás
A csoport célja optimalizálási problémákra olyan hatékony algoritmusok kidolgozása, amelyek optimális megoldást vagy jó közelítést találnak. Ezzel párhuzamos cél az új elméleti kérdésekben és alkalmazásokban felmerülő feladatok bonyolultságának meghatározása, illetve az ismert megoldó módszerek elemzése, továbbfejlesztése. Aktuális témáink között szerepel: kommunikációs hálózatok hibavédelmi mechanizmusai, Newton típusú algoritmusok az inverz optimalizálásban, paraméteres algoritmusok multivágás feladatokra, algoritmusok és strukturális eredmények hálózatok lokalizációs problémáira.
Vezető:
Jordán Tibor
Tagok:
Bérczi-Kovács Erika, Bérczi Kristóf, Fraknói Ádám, Gyimesi Péter, Király Tamás, Lydia Mendoza, Schwarcz Tamás, Szabó Dániel

PIT Bioinformatikai csoport
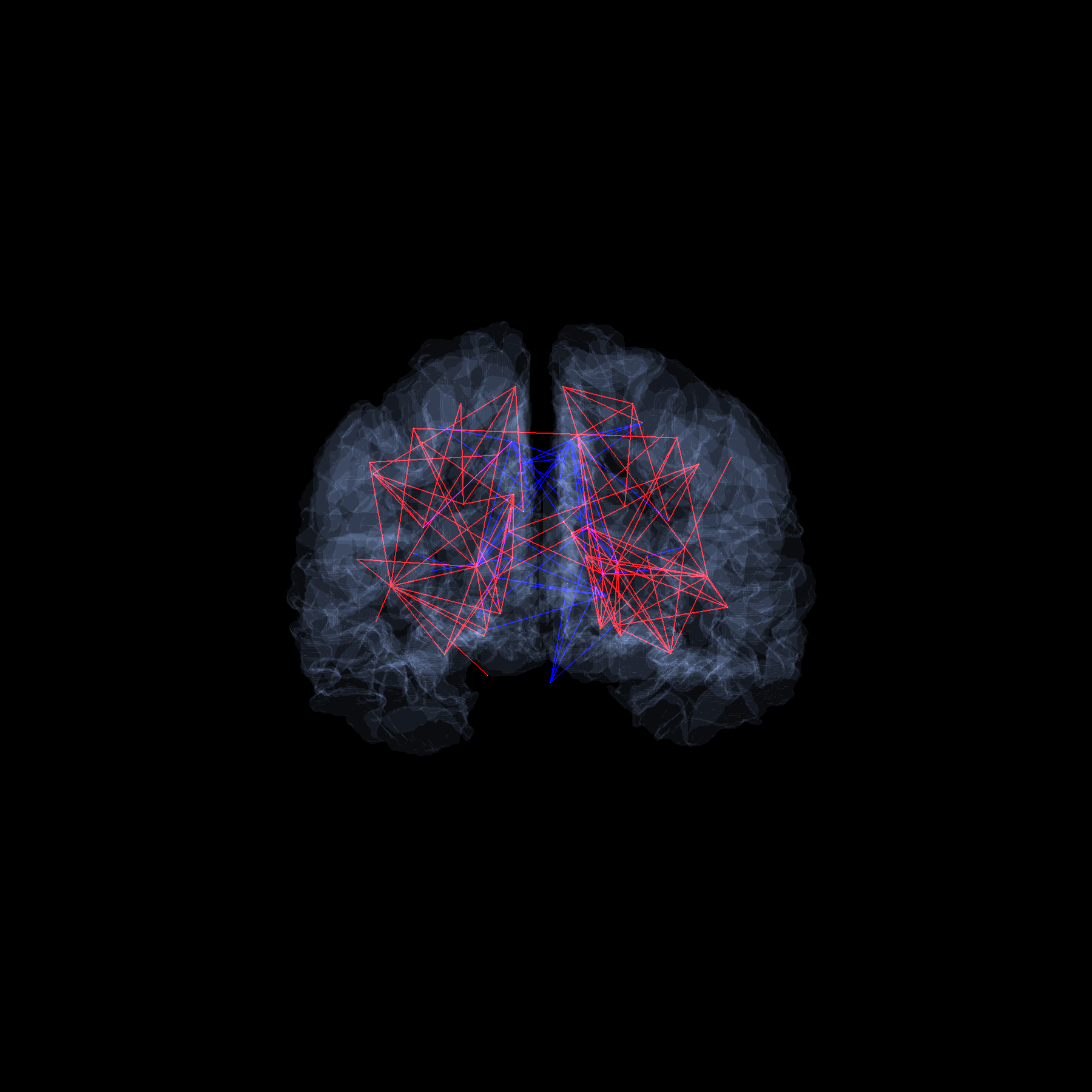
Új bioinformatikai eszközöket fejlesztünk és alkalmazunk fehérjehálózatok, az agy hálózata valamint molekulák strukturális tulajdonságainak tanulmányozására.
Vezető:
Grolmusz Vince
Tagok:
Bán-Szabó Áron, Hegedűs Dániel, Takács Kristóf, Varga Bálint

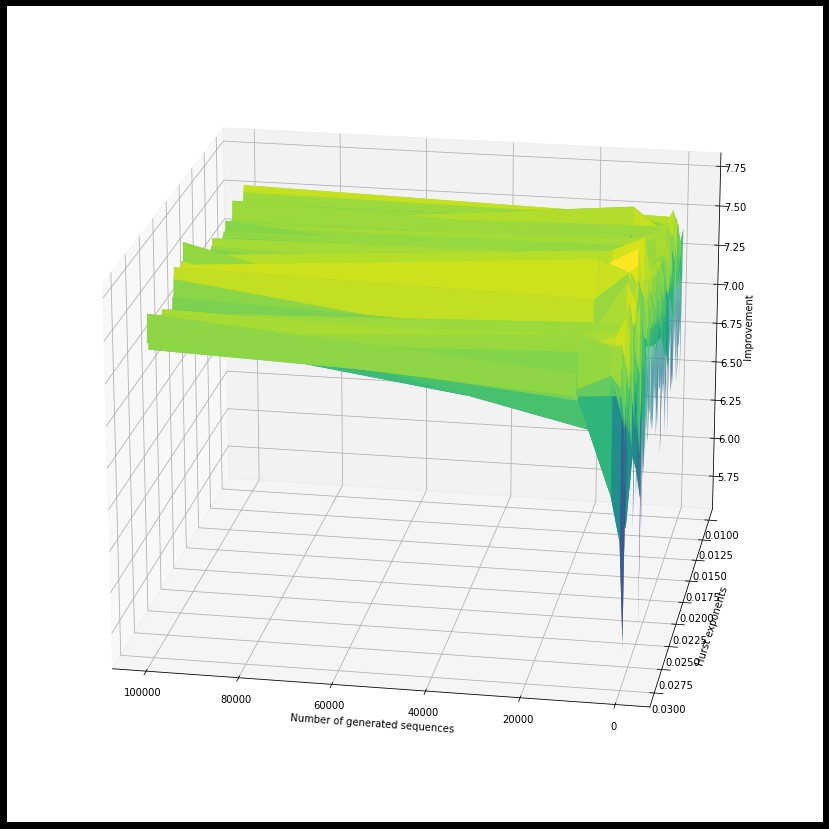
Pénzügyi matematika
Ebben az évben a Langevin algoritmust vizsgálják. Aszmiptotikus konfidenciaintervallumokat konstruálnak abban az esetben is, amikor az adatfolyam elemei nem függetlenek.
Vezető:
Rásonyi Miklós
Tagok:
Arató Miklós, Boros Dániel, Ivkovic Iván, Kovács Dávid, Martinek László, Márkus László, Nagy Lóránt, Tóth-Lakits Dalma
Hírek
-2024. február 12.: Fontos kérdés különböző síkbeli alakzatokra és görbékre azt vizsgálni, hogy hány olyan pár lehet, mely érinti egymást A kombinatorikus geometria kutatócsoport munkatársainak sikerült megmutatniuk, hogy ha adott a síkon két görbecsalád úgy, hogy mindkét család n darab páronként diszjunkt görbéből áll, akkor a köztük lévő érintések száma nagyságrendileg akár n(4/3) is lehet. Belátták, hogy ha a görbék páronként legfeljebb egyszer metszik egymást, akkor lineáris a nagyságrend. Ha a görbék x-monotonak, akkor Pach, Suk, and Treml eredményét megjavítva belátták, hogy a pontos nagyságrend nlog n.
Amikor csak egy n görbéből álló család van, melyben olyan görbék vannak, amik páronként legfeljebb t-szer metszik egymást, akkor azt sikerült megmutatniuk, hogy a köztük levő érintések száma nagyságrendileg legfeljebb n(2-1/(t+3)).
Pach egy sejtése szerint egy olyan görbecsalád, melyben minden görbepár vagy keresztezi egymást egyszer vagy érinti egymást egyszer, maximum lineárisan sok érintést definiálhat (a görbék számához mérten). Ezt sikerült bebizonyítani abban az esetben, ha a görbék x-monotonak.
Grünbaum 1972-es sejtése szerint két páronként metsző pszeudokör család (olyan zárt görbék, melyek páronként legfeljebb kétszer metszik egymást) legfeljebb 2n-2 érintést - avagy ekvivalensen üres metszetet - definiál. Lineáris felső korlátok már ismertek voltak, de a pontos felső korlát több, mint 50 éve nyitott kérdés. Az üres metszetes megfogalmazást sikerült megoldaniuk abban a speciális esetben, amikor a pszeudokörök igazi körök. A sejtés teljes megoldása pszeudokörökre is már egy folyamatban levő munka. A témában elért eredményeket bemutató legfrissebb, [3] cikk a napokban jelent meg (open access) online.
Hivatkozott cikkek:
[1] E. Ackerman, B. Keszegh, D. Pálvölgyi: On tangencies among planar curves with an application to coloring L-shapes, European Journal of Combinatorics, special issue dedicated to EuroComb 2021 (2023), https://doi.org/10.1016/j.ejc.2023.103837; Proceedings of EuroComb 2021, Trends in Mathematics - Research Perspectives CRM Barcelona Vol.14 (2021), 123-128. arXiv
[2] B. Keszegh, D. Pálvölgyi: The Number of Tangencies Between Two Families of Curves, Combinatorica 43 (2023), 939-952., arXiv
[3] E. Ackerman, B. Keszegh: On the number of tangencies among 1-intersecting x-monotone curves, European Journal of Combinatorics 118 (2024), https://doi.org/10.1016/j.ejc.2024.103929Conference version: E. Ackerman, B. Keszegh: On the number of tangencies among 1-intersecting curves, Proceedings of EuroComb 2023, Masaryk University Press (2023), 4-11., arXiv
[4] Eyal Ackerman, Gábor Damásdi, Eric Gottlieb, Balázs Keszegh, Rom Pinchasi, Rebeka Raffay: On the number of digons in arrangements of pairwise intersecting circles, SoCG 2024, accepted.
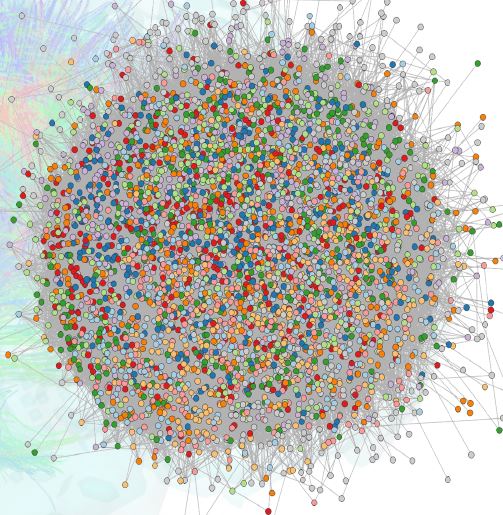 -2024. február 1.: Január 31-én rendeztük a projekt szokásos félévzáró worskhopját. A kutatócsoportok 19 előadást tartottak, mindenki bemutatta az aktuális kutatásait. Néhány érdekesebb téma: a bioinformatikai kutatócsoportunk elkezdte az OASIS3 adatbázis feldolgozását: ebben több, mint 1000 páciens agyi MRI félvételei találhatóak. Az agygráfok elemzése olyan kérdésekre adhat választ, mint az Alzheimer kór kialakulásának kockázata. A mély tanulás kutatócsoport nagy nyelvi modelleket ötvözött kisebbekkel, és így sikerült költséghatékonyan az eddigi legjobb teljesítményeket meghaladni szentiment elemzésben. A bemutatott megközelítés a legkülönfélébb feladatok esetében lehetőséget ad arra, hogy a kisebb erőforrással rendelkező felhasználók nagy adathalmazok esetében is ki tudják használni a legújabb nyelvi modellek képességeit. A bemutatott eredmények megmutatták, hogy a neurális hálózatokat sok tudományterületen eredményesen alkalmazzák kutatóink a differenciálegyenletektől a pénzügyi modelleken át az anyagtudományig.
-2024. február 1.: Január 31-én rendeztük a projekt szokásos félévzáró worskhopját. A kutatócsoportok 19 előadást tartottak, mindenki bemutatta az aktuális kutatásait. Néhány érdekesebb téma: a bioinformatikai kutatócsoportunk elkezdte az OASIS3 adatbázis feldolgozását: ebben több, mint 1000 páciens agyi MRI félvételei találhatóak. Az agygráfok elemzése olyan kérdésekre adhat választ, mint az Alzheimer kór kialakulásának kockázata. A mély tanulás kutatócsoport nagy nyelvi modelleket ötvözött kisebbekkel, és így sikerült költséghatékonyan az eddigi legjobb teljesítményeket meghaladni szentiment elemzésben. A bemutatott megközelítés a legkülönfélébb feladatok esetében lehetőséget ad arra, hogy a kisebb erőforrással rendelkező felhasználók nagy adathalmazok esetében is ki tudják használni a legújabb nyelvi modellek képességeit. A bemutatott eredmények megmutatták, hogy a neurális hálózatokat sok tudományterületen eredményesen alkalmazzák kutatóink a differenciálegyenletektől a pénzügyi modelleken át az anyagtudományig.
Az előadások diasorai itt találhatóak: https://drive.google.com/drive/folders/19EWZh-3h6JzHwDn6brpUFpLXFRfQtBnZ?usp=drive_link
-2024. január 24.: Kommunikációs hálózatok gerinchálózatainál felmerülő probléma az összeköttetések meghibásodásainak kezelése. A vizsgált problémában célunk minél több kommunikációs útvonalat meghatározni két pont között úgy, hogy egy potenciális meghibásodás legfeljebb egy utat blokkoljon. A probléma NP-nehéz, ha feltesszük, hogy egy-egy hibaesemény a hálózat több elemét is érintheti. Hálózattervezés során azonosítják az ilyen, együttes meghibásodásra hajlamos hálózati elemek csoportjait, melyeket SRLG-knek (Shared Risk Link Groups) nevezünk. Egy síkba lerajzolt hálózat esetén regionális SRLG-ről beszélünk abban az esetben, ha a sík egy összefüggő régiója (pl. körlap) által metszett összeköttetések alkotják a csoportot. Kutatásunkban regionális-SRLG-diszjunkt, nem keresztező utak maximális számát határoztuk meg két adott pont között. Eredményünk egyrészt általánosítja a korábbi megközelítéseket, másrészt egyszerűbb, gyorsabb, könnyen implementálható keretrendszert ad. Az elméleti eredményekből az első additív közelítés is adódik a probléma általánosabb NP-nehéz verziójára. Eredményeinket az IEEE International Conference on Computer Communications (INFOCOM) 2024 konferencián mutatjuk be. [Efficient Algorithm for Region-Disjoint Survivable Routing in Backbone Networks - Erika R. Bérczi-Kovács (ELTE, Eötvös Loránd University, Hungary); Péter Gyimesi (ELTE, Eötvös Loránd University, Hungary); Balázs Vass and János Tapolcai (Budapest University of Technology and Economics, Hungary)].http://lendulet.tmit.bme.hu/lendulet_website/wp-content/papercite-data/pdf/berczi-kovacs2024efficient.pdf.
-
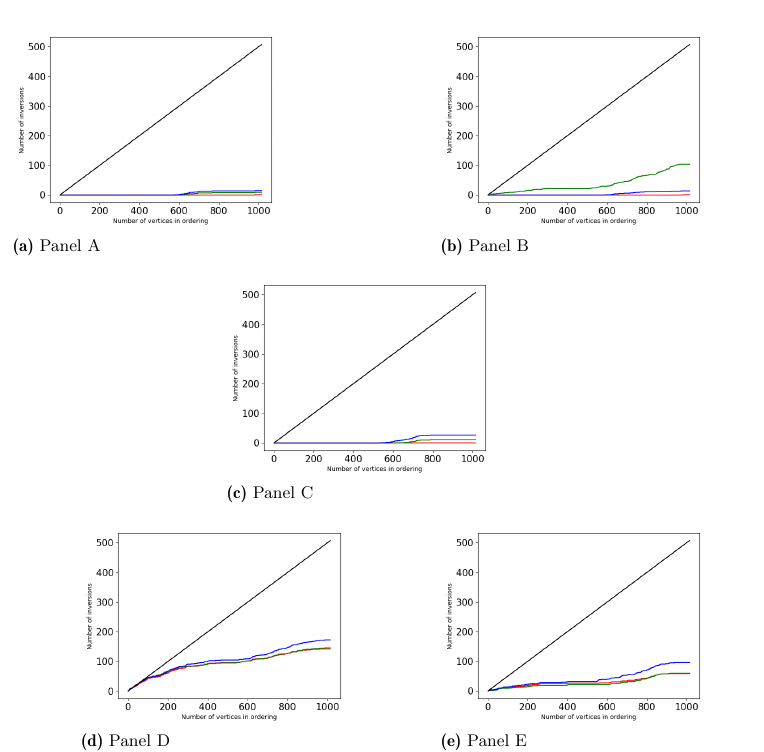 2024. január 18.: Hegedűs Dániel és Grolmusz Vince az ELTE PIT Bionformatikai Csoport kutatói, a csoport által kiszámolt, több, mint 1000 alany agyi összeköttetéseit vizsgálva megállapították, hogy több, különböző csúcs-fontossági sorrend között csupán kis különbségek vannak csak. A csúcsok a különböző agyi területeknek felelnek meg, és két agyi területet éllel kötünk össze akkor, ha idegrostokat találunk köztük az MRI felvételek elemzése során. A fontossági sorrendek megállapításánál olyan paramétereket vettek számításba, mint a csúcs (1) fokszáma, (2) a csúcsból induló élek vastagságainak összege, (3) ezek maximuma, vagy (4) ezek átlagos vastagsága, a (5) csúcsból induló élek hosszainak összege, illetve (6) ezek maximuma, vagy (7) átlagos hosszúsága.
A mellékelt ábrákon a különböző sorrendeket hasonlítják össze, a fekete átlós egyenes a véletlen sorozatok esetében számolt inverziós számok várható értékét jelzi a legfontosabb csúcsokhoz képest, a színes vonalak a különböző fontossági sorrendek összehasonlításának inverziós számait jelzik (részletek a cikkben, I. ábra): minél laposabbak a színes vonalak, annál kisebb a különbség a sorrendek közt.
A publikáció 2024. január 17-én jelent meg a PLOS One folyóiratban: https://doi.org/10.1371/journal.pone.0292613.
2024. január 18.: Hegedűs Dániel és Grolmusz Vince az ELTE PIT Bionformatikai Csoport kutatói, a csoport által kiszámolt, több, mint 1000 alany agyi összeköttetéseit vizsgálva megállapították, hogy több, különböző csúcs-fontossági sorrend között csupán kis különbségek vannak csak. A csúcsok a különböző agyi területeknek felelnek meg, és két agyi területet éllel kötünk össze akkor, ha idegrostokat találunk köztük az MRI felvételek elemzése során. A fontossági sorrendek megállapításánál olyan paramétereket vettek számításba, mint a csúcs (1) fokszáma, (2) a csúcsból induló élek vastagságainak összege, (3) ezek maximuma, vagy (4) ezek átlagos vastagsága, a (5) csúcsból induló élek hosszainak összege, illetve (6) ezek maximuma, vagy (7) átlagos hosszúsága.
A mellékelt ábrákon a különböző sorrendeket hasonlítják össze, a fekete átlós egyenes a véletlen sorozatok esetében számolt inverziós számok várható értékét jelzi a legfontosabb csúcsokhoz képest, a színes vonalak a különböző fontossági sorrendek összehasonlításának inverziós számait jelzik (részletek a cikkben, I. ábra): minél laposabbak a színes vonalak, annál kisebb a különbség a sorrendek közt.
A publikáció 2024. január 17-én jelent meg a PLOS One folyóiratban: https://doi.org/10.1371/journal.pone.0292613.- 2023. szeptember 25-29.: Lukács László előadás-sorozatot tartott a gépi tanulás aktuális témáiról. Az előadások diái itt érhetőek el.
- 2023. július 5.: Összesen 22 előadás hangzott el az ezúttal jelenléti formában tartott évzáró workshopunkon.
- 2023. június 26.: Fekete Imre és Izsák Ferenc közönséges és parciális differenciálegyenletek neurális háló alapú numerikus megoldásai témakörben miniszimpóziumot szervezett a Lengyelországban tartott 22. Európai Ipari Matematikai Konferencián.
- 2023. február 14.: Sikeresen lezajlott a félévnyitó workshop, ahol közel 30 előadásban foglalták össze a kutatócsoportok az elért eredményeiket és egyúttal bemutatkoztak az újonnan csatlakozó kutatók is.
- 2022. december 9.: Arató Miklós és munkatársai Kennedy típusú véletlen mezők statisztikai vizsgálata, valamint sztochasztikus tartalékolási módszerek összehasonlítása témakörökben publikáltak
- 2022. november 21.: Backhausz Ágnes a POPNET Connects szemináriumon tartott előadást.
- 2022. augusztus 19.: Új nagyteljesítményű számítógép segíti az ELTE Matematikai Intézetében a Mesterséges Intelligencia kutatócsoportot
A nyáron beüzemeltük a projektből beszerzett szerver gépet, amelyben 8 nagyteljesítményű grafikus processzor és 1,8 Terabyte memória gondoskodik a világszínvonalú teljesítményről. Az új gép fő profilja a már működő programok hatékony futtatása lesz, elsősorban a képfeldolgozás, a differenciálegyenletek és a természetes nyelvfeldolgozás, valamint a pénzügyi modellezés területén. Minden bizonnyal több területen is sikerülni fog érdeklődésre számot tartó eredményeket elérni az új gép segítségével – ezekről ezeken a hasábokon is hírt fogunk adni a jövőben.
- 2022. július 6.: Backhausz Ágnes az ELTE Kárpát-medencei Magyar Nyári Egyetemén népszerűsítő előadást tartott.
- 2022. június 29.: A projekt félévzáró workshopja
- 2022.június 7-10. Fekete Imre, Izsák Ferenc és Simon Péter szervezésében sikeresen lezajlott 12 ország részvétele mellett 26 előadással a 6th Workshop on Stability and Discretization Issues in Differential Equations c. workshop.
- 2022. április 20: Izsák Ferenc a Rényi Intézetben tartott előadást
Tagok
Oktatók és kutatók
Tanársegéd

Villányi Viktória
Adjunktus
Doktoranduszok és hallgatók
Hallgató
Hallgató

Doktorandusz

Ivkovic Iván
Doktorandusz

Hallgató
Hallgató
Doktorandusz
Hallgató
Doktorandusz

Doktorandusz
Doktorandusz
Doktorandusz
Doktorandusz
Doktorandusz
Hallgató
Ugi Gábor
Hallgató
Vass Bernadett
Hallgató
A kutatás az Innovációs és Technológiai Minisztérium Nemzeti Kutatási, Fejlesztési és Innovációs Alapból nyújtott támogatásával, a Nemzeti Kutatási, Fejlesztési és Innovációs Hivatal által kibocsátott ELTE TKP2021-NKTA-62 sz. támogatói okirat alapján valósult meg.
Kapcsolat
Cím:
1117, Budapest, Pázmány Péter sétány 1/C
Telefonszám:
+36 1 381 2202
Email:
mathinst[ ]math.elte.hu


























