AI Research Group – Artificial Intelligence & Data Science

AI Research Group

Artificial Intelligence & Data Science

“This is only a foretaste of what is to come, and only the shadow of what is going to be.”

About us

The research group was established to provide a knowledge and know-how center at the Eötvös University in the state-of-the-art AI techniques. This initiative is a joint effort of the Department of Computer Science, Institute of Mathematics, Eötvös Loránd University and the Alfréd Rényi Institute of Mathematics, Eötvös Loránd Research Network.

At the Department of Computer Science, Institute of Mathematics, Eötvös Loránd University AI, data and network science have been an active topic of research and teaching for more than a decade. We have a long tradition and expertise in modelling, solving problems and use-cases from a wide range of domains. We work with with the objective of keeping up a good balance of mathematical and engineering approach. Our expertise was called in several R&D projects from the fields of telecommunication, finance, security and also life sciences.

Machine/Deep Learning competencies includes the state-of-the-art image, sequential and textual data analysis and retrieval techniques; unsupervised learning; and generative and adversarial approaches. Further special strengths of the department are combinatorics, graph/network theory and algorithms, optimization and their applications.

The research group is involved two larger AI R&D initiatives. The first is the AI4EU project aiming to build the European AI on-demand platform, a hub for AI applicators and researchers in the European AI ecosystem. As the member of the AI4EU consortium, our tasks are doing research on AI and building of the AI4EU community. The AI4EU project is supported by the European Union under the Horizon 2020 program, grant No. 825619.

The other project on the mathematical tools and theory of artificial intelligence, especially of machine and deep learning. A direction of research is to bridge the gap between mathematical theory and machine learning practice by exploiting newly discovered deep connections between fundamental results related to the study of large networks and the more applied domain of machine learning. Additionally, pilot interdisciplinary projects are realized that may directly demonstrate the practical applicability of the theoretical research. The project entitled The mathematical foundations of artificial intelligence runs under the frame of the National Excellence Program 2018-1.2.1-NKP of the Hungarian Research, Development and Innovation Office, between 2019 and 2021.

Deep Learning

Data Science

Network Science

Visual Analytics

Research

Automated theorem proving

Automated Theorem Proving (ATP) and Deep Learning (DL) are two important branches of artificial intelligence both of which have undergone huge development over the past decade. A novel and exciting research direction is to find a synthesis of these two domains. One possible approach is to use an intelligent learning system to guide the theorem prover as it explores the search space of possible derivations. Our group tackled the question of how to generalize from short proofs to longer ones with a strongly related structure. This is an important task since proving interesting problems typically requires thousands of steps, while current ATP methods are only finding proofs that are at most a couple dozens of steps long.

The project has a homepage and a public code repository. This work has been presented at the Bumerang workshop, the Conference on Artificial Intelligence and Theorem Proving and the Dagstuhl Logic and Learning Seminar. A paper about this project is currently under review, and was accepted as oral presentation for the Knowledge Representation & Reasoning Meets Machine Learning Workshop at NeurIPS 2019.

Autoencoders and representations

Wasserstein Autoencoders are autoencoders with the extra goal of making the pushforward (the latent image) of the data distribution close to some prior. For such models, the regularization term enforcing this closeness is based on the latent image of a single minibatch. (In effect, it is some normality test statistic based on a single minibatch as test sample.) We argue that when the size of the minibatch is of the same magnitude as the latent dimension, such statistics are not powerful enough. Our ongoing project investigates models where the regularization term is a function of the latent image of the full dataset.

Differential equations and DNNs

In the last years, an interim connection was explored between neural networks and differential equations.

It was recognized that inculding new layers can correspond to taking a numerical approximation of ODE’s such that the original problem can be associated with solving an appropriate ODE. The main objective in this research direction is to understand how can we use this correspondence to speed up the training of the original DNN.

On the other hand, some numerical approximations of ODE’s can be given as a neural network. A feasible training then can result in the optimal NN, which is an optimal numerical solution. What we can do without any training data, as the solution is unknown? Here our aim is to find an implement feasible loss functions which can be the basis of an efficient learning process.

Medical image computing

Within the medical industry, medical imaging is one of the most prominent industries where deep learning can play a huge role. The aim of our research is twofold: first, to develop solutions to pressing problems within the field such as inconsistent inter-rater reliability and the declining amount of practicing radiologists by introducing deep learning backed automation in the diagnostic pipeline, secondly to improve upon existing state-of-the-art methods by studying the application of Generative Adversarial Networks (GANs) to medical imaging data. Currently we are researching structure-correcting adversarial networks on X-ray segmentation tasks, as well as super-resolution methods on computed tomography scans.

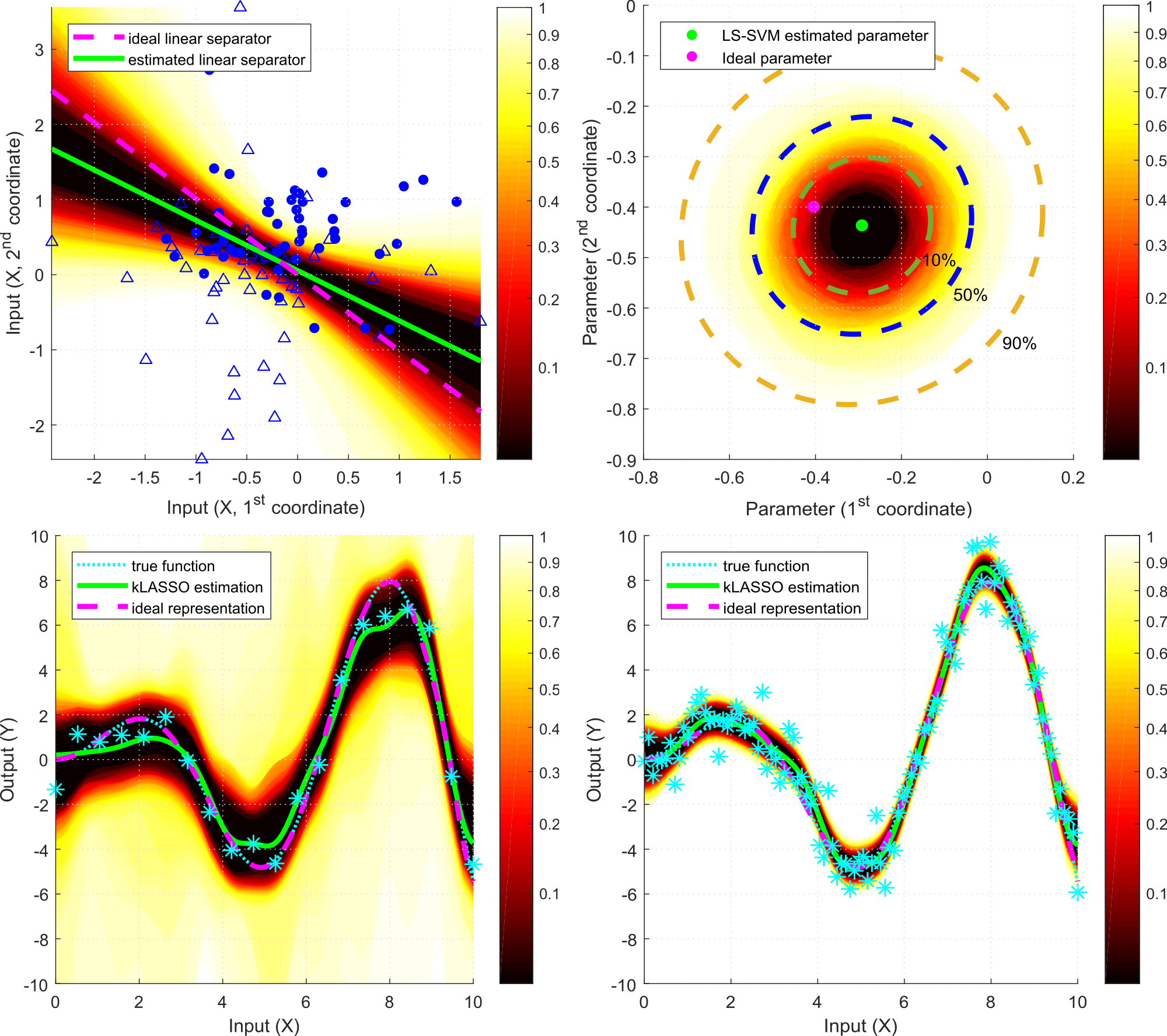
Statistical Learning Theory

Statistical learning theory is a machine learning framework to study empirical inference. It mainly draws from the fields of mathematical statistics, functional analysis and operations research. The field includes both supervised (such as classification and regression) and unsupervised (for example, clustering and anomaly detection) learning approaches, and it often aims at designing algorithms with probably approximately correct (PAC) type guarantees. One of the fundamental problems of statistical learning is to provide guarantees for the generalization capabilities of models, namely, building on a finite sample of observations, how well the estimated model performs on unseen measurements. Kernel methods, including support vector machines, are among the fundamental tools of the field. Their mathematical foundations are based on the theory of Reproducing Kernel Hilbert Spaces (RKHSs), and the resulting estimation methods often lead to uncertain convex optimization problems. We are interested in statistical learning methods with strong non-asymptotic and distribution-free guarantees. Our main fields of interest are randomized algorithms (such as resampling), nonparametric confidence and prediction regions, stochastic approximation (online learning), and (conditional) kernel mean embedding of distributions.

Natural Language Processing

TBW

Log analysis and self-healing of networks

TBW

Study Groups

Stochastic correlation estimation

The correlation between prices and values of certain financial instruments is time-dependent that can change stochastically. These recognitions have changed the modeling practice of the last decade, by introducing a stochastic process – called stochastic correlation.

In most cases, the estimation of these models’ parameters requires very complex, computation-intensive Monte-Carlo algorithms, and therefore we should look for alternatives. Hence, we invoke neural network models that we utilize to estimate the parameters of the correlation process. We investigate different networks as well as the effects of different loss functions, activation functions and optimizers.

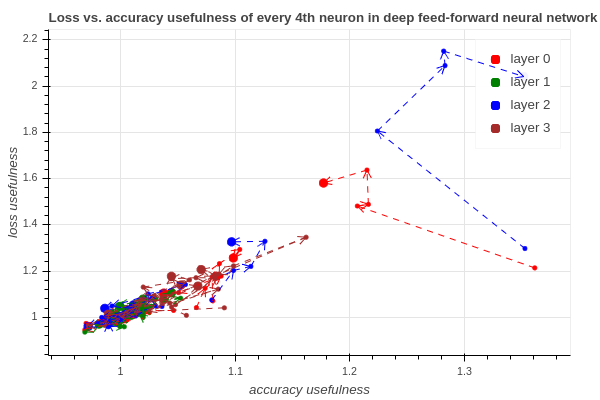
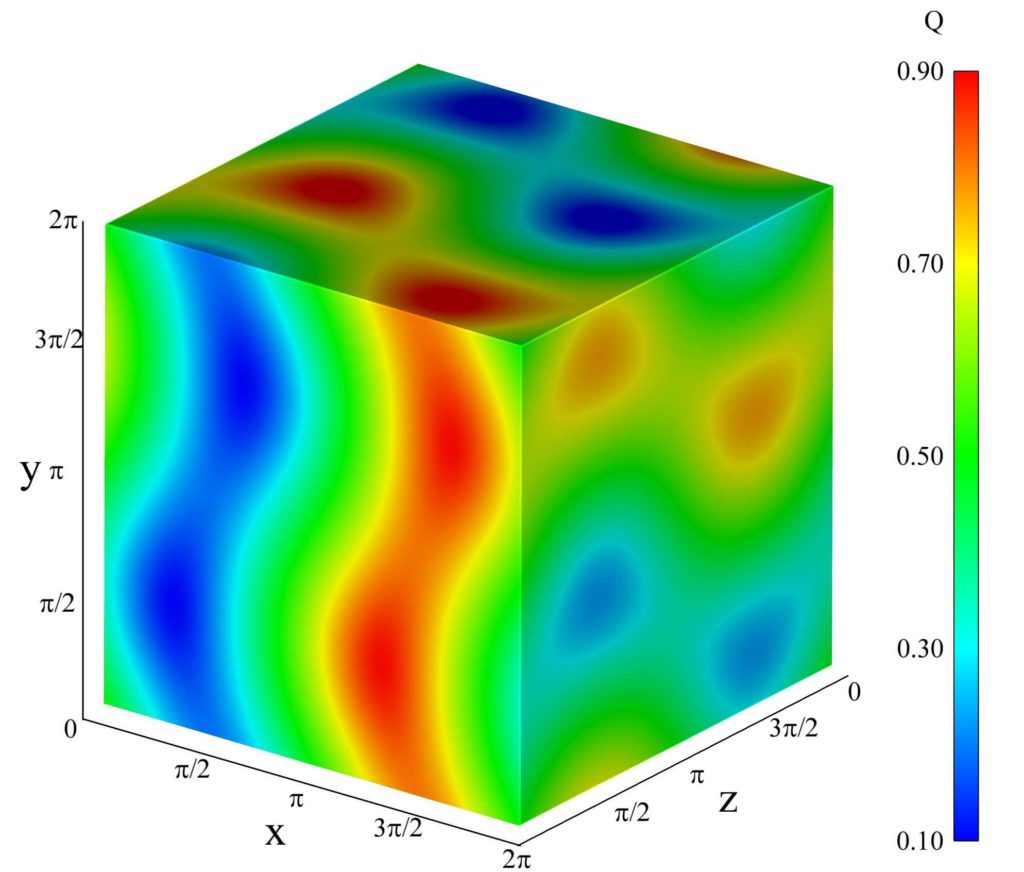
Usefulness of neurons

We are interested in whether some neurons in a neural network can be classified as useful and useless. We aim to predict this usefulness during the training phase of the neural network, ideally using some easy-to-calculate methods. This interactive visualization shows one of our first results that the usefulness based on the loss or on the accuracy is correlating. Our current method is able to predict the established usefulness measure using only the network’s inside data during the training phase. The codebase of this project can be found here.

Model visualization

Deep neural networks were considered notoriously opaque, hard to interpret systems for a long time, but in the last few years, deep dream based algorithms made great progress in helping us understand the internal structure of trained vision models. These algorithms do gradient ascent on pixel inputs to maximize neuron activation. Our aim is to understand deep vision models better by utilizing such tools. One area that is to the best of our knowledge is currently uncharted is transfer learning: how specific neurons adapt when the classification task changes, say, from classifying animals to classifying flowers?